Je Pi polynóm?

Video: Je Pi polynóm?

2024 Autor: Lynn Donovan | [email protected]. Naposledy zmenené: 2023-12-15 23:52

Pi (π) sa nepovažuje za a polynóm . Je to hodnota vzťahujúca sa na obvod kruhu. Na druhej strane, polynóm sa týka rovnice obsahujúcej štyri alebo viac premenných.

Môže byť pi súčasťou polynómu?

Odpoveď je NIE. Ak tam bol a polynóm s algebraickými koeficientmi by existoval aj a polynóm s racionálnym koeficientom (s väčším stupňom). Je to preto, že ˉQ je algebraicky uzavreté. Predpokladajme, že π boli koreňom a polynóm f(x)=xn+an−1xn−1+⋯+a0, pričom ai sú algebraické čísla.

Po druhé, čo tvorí polynóm? V matematike a polynóm je výraz pozostávajúci z premenných (tiež nazývaných neurčité) a koeficientov, ktorý zahŕňa iba operácie sčítania, odčítania, násobenia a nezáporných celých exponentov premenných. Príklad a polynóm z jednej neurčitej, x, je x² − 4x + 7.

Je Pi v tomto ohľade Monomial?

Áno, π π je a monomiálny pretože je to číslo.

Musí mať polynóm premennú?

Takže: A polynóm môcť mať konštanty, premenných a exponenty, ale nikdy delenie a premenlivý . Tiež môžu mať jeden alebo viac termínov, ale nie nekonečný počet termínov.

Odporúča:

Ako sa nazýva polynóm so 6 členmi?

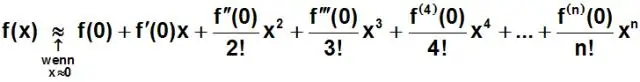
K polynómom sa priraďujú tieto názvy podľa ich stupňa: Stupeň 4 – kvartický (alebo, ak majú všetky pojmy párny stupeň, bikvadratický) Stupeň 5 – kvintický. Stupeň 6 – sextický (alebo menej často hexický)

Čo je to polynóm prvého stupňa?

Polynómy prvého stupňa. Polynómy prvého stupňa sú známe aj ako lineárne polynómy. Najmä polynómy prvého stupňa sú čiary, ktoré nie sú ani horizontálne, ani vertikálne. Častejšie sa písmeno m používa ako koeficient x namiesto a a používa sa na vyjadrenie sklonu čiary